tecznotes

I spent days eight and nine in Chicago. Walking Papers is up in all its crinkly glory at the Chicago Art Institute, in the Hyperlinks exhibit thanks to curator Zöe Ryan. Eric, Geraldine, and intern Martha Pettit arranged a selection of submitted scans over a twelve foot wall. It was bitterly cold, and I thought I’d do a much better job of getting out and about without being quite prepared for the reality of weather. Adrian, Paul, and the gang at Everyblock kindly offered a bit of couch space at their northside office for me to lounge on during day nine, and when I left I saw a tiny rabbit cross my path in the snow. I’m told that’s normal - “lots of friendly squirrels and bunnies in Chicago.”

Day ten was travel, and movies, and general laziness. I launched the Atlas feature of Walking Papers, which you can see if you compose a new scan on the front page. You get back a multi-page PDF; nothing special but the possibility of using these to distribute assignments to a group is something I’ve been planning for. Since I last mentioned it, the Random Hacks Of Kindness TaskMeUp project popped onto my radar - it seems to be built around some of the same ideas, aiming for the world of humanitarian and crisis response.

The thing that really ate my head for the past few days has been a computational geometry technique called the straight skeleton. The short story is that it’s a way to simplify polygons down to lines with special applications for cartography. The long story is that I have a personal history of letting what Aaron calls “mathshapes” consume me for days on end, and this is the latest example. Some people have knitting, crossword puzzles, gambling, or crack. I have geometry, and my biggest personal challenge during a fairly open-ended sabbatical like this one has been to ensure that when even whean heading down blind alleys, there’s a plan for sharing the results.

Anyway, this is a simplified illustration (from my State Of The Map U.S. conferences slides) that shows how the use of buffers, polygons, and the straight skeleton can be used to convert OpenStreetMap road data into improved, more easily-labeled lines:

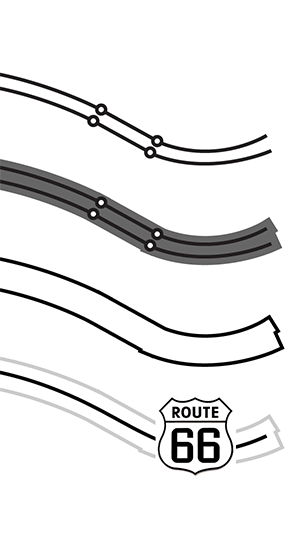
As I mentioned in my NACIS keynote last year, OpenStreetMap has a fairly specific range of scales where it’s designed to work best, and if you need to create a lower-zoom map you will find that details like dual carriageways (large roads and freeways split into parallel strips) and interruptions for bridges or tunnels make it incredibly hard to generate good looking labels, not to mention the issue of publishing raw data in a useful or compressed form. While deriving the skeleton of a shape is perfect for this problem, there’s not a lot out there in the way of accessible implementations of the algorithm. OpenStreetMap has no current answer to the idea of derived, lower-resolution datasets outside the very low-resolution Natural Earth collection. OSM is historically biased toward manual production, and Steve Coast has advised me that setting up lower resolution OSM servers for manual tracing might be a more sensible way to handle this unmet need. I do agree, though computed geometries offer an excellent leg up to solve the cold start problem somewhat.

So, I blew through two days reading through implementation notes and doing a bit of coding, starting from Tom Kelly’s java implemetation Campskeleton. I’m not a java programmer, but Kelly’s straight skeleton index page offers plenty of notes on how to actually get the thing built. Most important are a few late-90s academic papers: Raising Roofs, Crashing Cycles, Playing Pool by David Eppstein and Jeff Erickson and especially Straight Skeleton Implementation by Petr Felkel and Štěpán Obdržálek, along with the cartography-specific approach from Using the Straight Skeleton for Generalisation in a Multiple Representation Environment.

Anyway, here’s where I’ve gotten to:

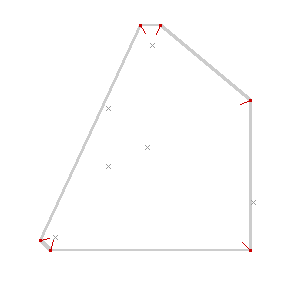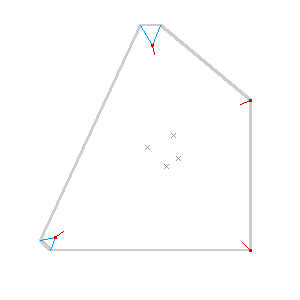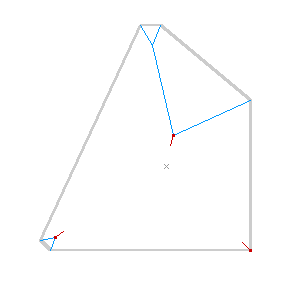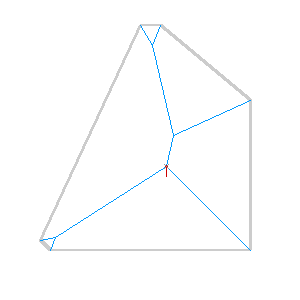
The easiest way to think of the straight skeleton is as a peaked roof on a building. Starting with the gutters of an arbitrarily-shaped building, you build up sloping roof until the bits all meet in the middle. The ridge of roof all the way around is the skeleton, and it gives a pretty good idea of the building’s axis, or a path it follows.

That angular blob might not look like a map, but imagine it as a curving road. Here’s what I’m aiming for, more generally:

The idea is similar in spirit to Paul Ramsey’s simplified Vancouver Island. There are a bunch of pitfalls in the process. Here’s one from before I figured out how to correctly order the priority list of roof line intersections, and didn’t check that points were actually inside the containing polygon:

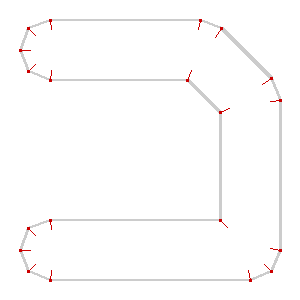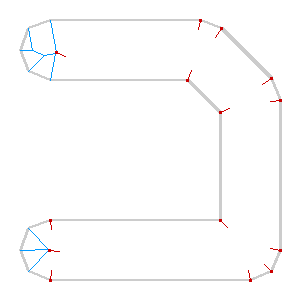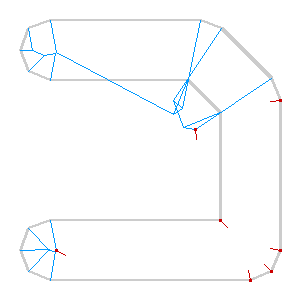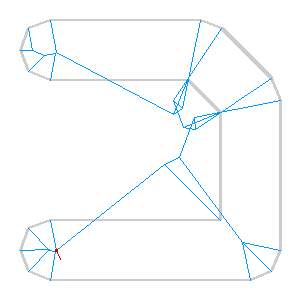
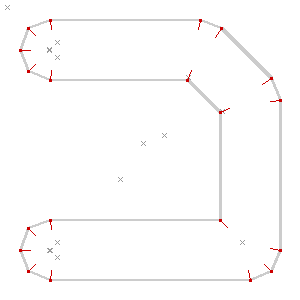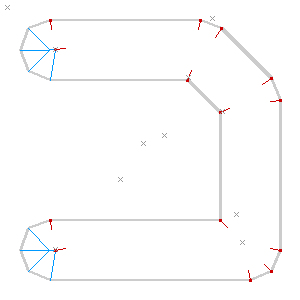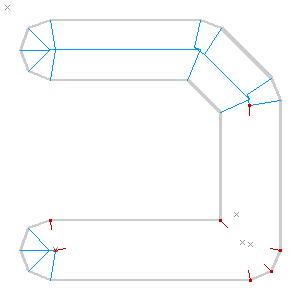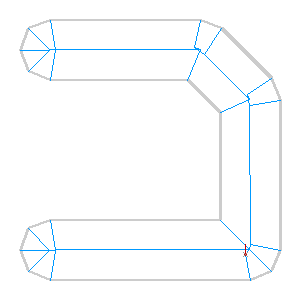
Here’s an example showing an imaginary dual carriageway, buffered out to merge the shapes into a single polygon and then skeletonized down the middle:

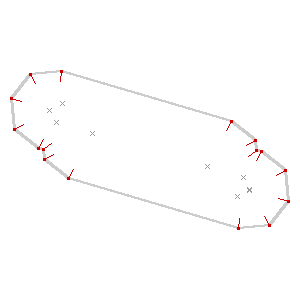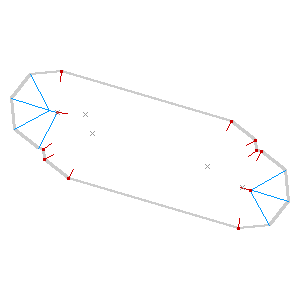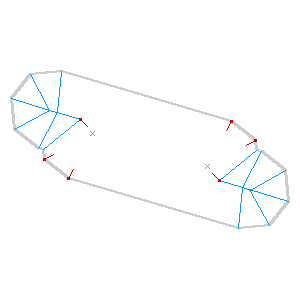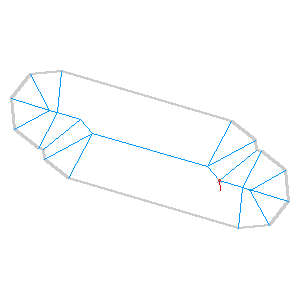
The algorithm is incredibly sensitive to initial conditions, such as this example where a few extra parallel lines result in a double-peaked roof. It’s a plausible overhead view of a building, and a correct skeleton, but not quite the thing for cartography:

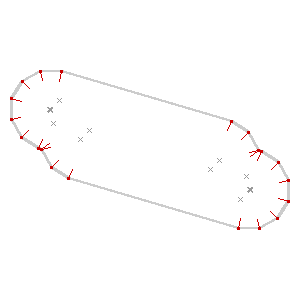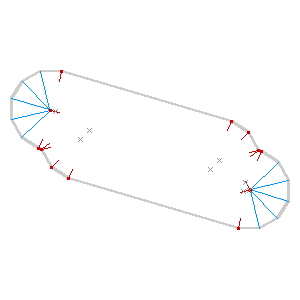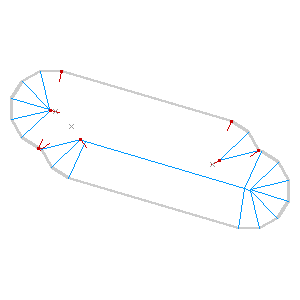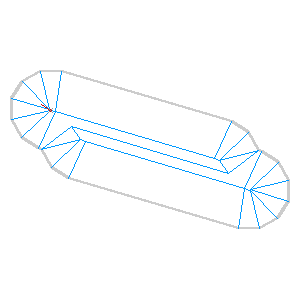
It’s also worth noting that I’m not doing anything to detect collisions just yet:

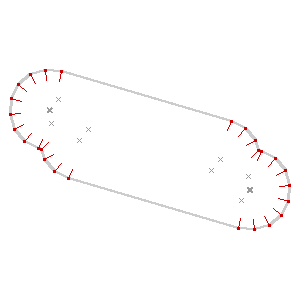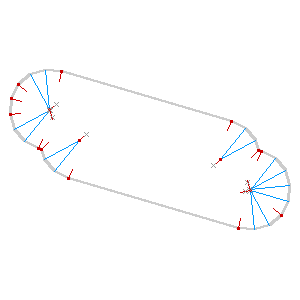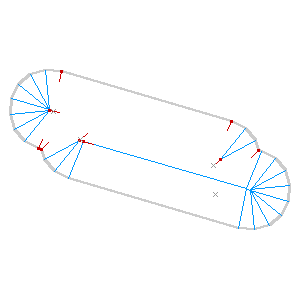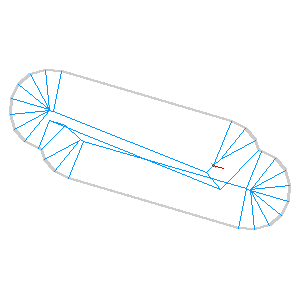
I’m getting close to done with this alley. The particular needs I’m aiming at are largely connected to the book-based bicycle map I described last time. It’s possible now to render excellent maps from OSM, but the medium of print makes small errors much more glaring, and I’m interested in fixing some of the loose ends of cartographic representation and OpenStreetMaps.

So, math shapes.